Determinación hamiltoniana de sistemas cuánticos a escalas mucho más pequeñas
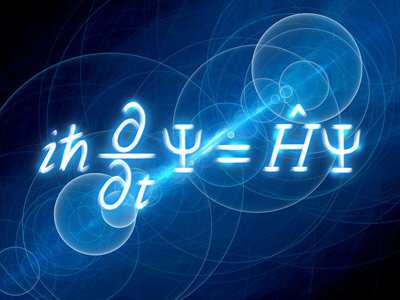
En el corazón de la ecuación de Schrödinger se encuentra el hamiltoniano (H). Los investigadores de RIKEN muestran que la cantidad de mediciones necesarias para determinar el hamiltoniano de un sistema cuántico aumenta a medida que aumenta el cubo de la cantidad de partículas en el sistema. Crédito: Biblioteca de fotos científicas
Los físicos de RIKEN y tres colaboradores han demostrado que la cantidad de medidas necesarias para describir un sistema de partículas cuánticas es mucho menor de lo que se pensaba anteriormente. Además de reducir la carga de trabajo de los experimentadores, este descubrimiento tiene implicaciones importantes para validar tecnologías cuánticas emergentes como la computación cuántica.
Todas las cosas que nos rodean son colecciones de partículas cuánticas unidas entre sí por fuerzas electromagnéticas. Estas fuerzas se pueden expresar a través de ecuaciones notablemente simples. La complejidad surge porque las interacciones entre partículas producen fenómenos cuánticos no triviales que no pueden expresarse en términos del comportamiento de una sola partícula.
“El mundo en el que vivimos se rige por la ecuación de Schrödinger”, explica Tomotaka Kuwahara del Centro RIKEN para el Proyecto de Inteligencia Avanzada. “En principio, podemos explicar todos los fenómenos de la naturaleza resolviendo esta ecuación. Pero para obtener la ecuación de Schrödinger, es necesario conocer el hamiltoniano (es decir, la matriz de energía), que depende de los detalles del sistema”.
El hamiltoniano se puede determinar realizando mediciones repetidas en un sistema cuántico. Pero con los algoritmos existentes, la cantidad de mediciones aumenta exponencialmente con la cantidad de partículas que componen el sistema, lo que lleva a una gran cantidad de experimentos.
Ahora, Kuwahara y tres colaboradores de IBM, UC Berkley y MIT en EE. UU. han desarrollado un sistema de aprendizaje automático. algoritmo en el que el número de medidas requeridas aumenta como un cubo de Número de partículas Su preparación tiene en cuenta la posición empíricamente relevante del número de copias del estado de Gibbs del objetivo hamiltoniano necesarias para determinar el hamiltoniano. Para un sistema de 15 partículas, son aproximadamente 3000 mediciones en lugar de unas 30 000, mientras que para un sistema de 100 partículas, son 1 000 000 de mediciones en lugar de 10.29.
Sorprendentemente, el resultado se aplica incluso a regímenes de baja temperatura, que balance térmico Los estados suelen tener estructuras muy complejas.
Este avance tiene implicaciones importantes para las computadoras cuánticas. “en un Estadísticas Cuantitativas, a menudo necesitamos especificar el sistema hamiltoni para comprobar; Kohara dice que dicha verificación es un problema crítico para la implementación confiable de algoritmos cuánticos. “Nuestro resultado se puede utilizar para verificar algunos algoritmos cuánticos importantes”.
Los investigadores también esperan que su algoritmo pueda usarse para investigar las propiedades de los materiales cuánticos mediante la realización de mediciones cuánticas. “Una aplicación de nuestro método es usarlo para dilucidar las propiedades de sistemas cuánticos exóticos que se realizan en estructuras complejas, como experimentos con átomos ultrafríos o experimentos con iones atrapados”, dice Kohara.
El equipo ahora planea expandir su trabajo en dos direcciones. “Al usar nuestras técnicas actuales, podemos aclarar la complejidad de una muestra de otros problemas de aprendizaje”, dice Kuwahara. “También queremos mejorar nuestro algoritmo para que la muestra no solo sea eficiente, sino que también ahorre tiempo”.
Anurag Anshu et al, Aprendizaje de muestra efectivo para sistemas cuánticos que interactúan, Física de la naturaleza (2021). DOI: 10.1038 / s41567-021-01232-0
La frase: Identificación hamiltoniana de sistemas cuánticos a escalas mucho más pequeñas (13 de enero de 2022) Recuperado el 13 de enero de 2022 de https://phys.org/news/2022-01-hamiltonian-quantum.html
Este documento está sujeto a derechos de autor. Sin perjuicio de cualquier trato justo con fines de estudio o investigación privados, ninguna parte puede reproducirse sin permiso por escrito. El contenido se proporciona únicamente con fines informativos.

“Defensor de la Web. Geek de la comida galardonado. Incapaz de escribir con guantes de boxeo puestos. Apasionado jugador”.
