Dos grupos de trabajo de la Universidad de Sevilla y la Universidad de Lehigh Ella fue la encargada de descubrir la última forma geométrica. Las formas de completar el espacio en blanco con piezas más pequeñas son infinitas. Con Los escotides plantearon otra pregunta: cómo se forman las células que llenan los tejidos epiteliales que forman parte de todos los animales. Así es como se ven y cómo se unen.

losLas células epiteliales son los componentes básicos de un animal. Son como piezas de Lego que se ensamblan para dar las formas más variadas. Esto no sucede de repente, sino poco a poco. Las células epiteliales se mueven y ensamblan de manera controlada durante el desarrollo embrionario.

Epitelización Necesario para hacer la transición desde la celda. (Cigoto) en una estructura simple que consta de Pocos y fetos para un individuo completo con órganos complejos. Este proceso es necesario, porque la función y la forma del órgano están relacionadas. Para que funcione bien, su forma debe configurarse correctamente.

Disposición de líneas

Las células aparecen en el epitelio de forma ordenada, muy próximas entre sí sin dejar huecos. Hasta ahora, se ha estudiado con tejidos simples que se pueden modelar mediante una representación plana. Además, se sabía que La forma y la disposición de las células en los tejidos se pueden aproximar mediante el diagrama de Voronoy.

“La descomposición de un área métrica en regiones relacionadas con la existencia de organismos, de tal manera que en esta descomposición antes mencionada, se asigna una región del área métrica a cada uno de los puntos que seMás cerca de él que cualquier otra cosaExplique a los profesionales de A. Investigación Publicado en Conversación.

En otras palabras, consiste en “Divida el área en tantas áreas como sea posible donde haya puntos u objetos de tal manera que el área se asigne a cada punto Señalando todo lo que está más cerca de él que nadie.

Hay otra forma de obtener diagramas de Voronoy. Dado un conjunto de puntos en el plano, si los círculos crecen alrededor de ellos al mismo ritmo, también se genera un diagrama de Voronoi.

Células epiteliales simples, planas y en crecimiento, Se empaqueta en 2D porque todo crece con la misma fuerza desde el mismo centro de masa. Esta idea ya ha sido aprovechada por Luisma Escudero, un profesional que es miembro del estudio y que dio el nombre de escutoide, para desarrollar un modelo que funcione para comprender cómo la organización de los tejidos afecta el desarrollo tumoral.

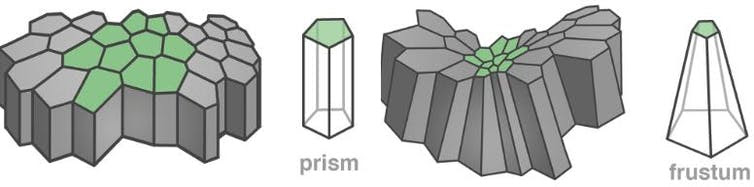
Escudero y colegas Cree un modelo ideal de tejido epitelial plano (y muscular) mediante un procedimiento computacional en el que primero se genera un conjunto de puntos aleatorios; Luego, para estos puntos se calcula su diagrama de Voronoi. Le sigue el centro de masa para cada una de las regiones resultantes (esto nos da un nuevo conjunto de puntos) y se calcula el diagrama de Voronoy para el nuevo conjunto.

El proceso se repite hasta tres veces más. El aspecto de este quinto diagrama de Voronoy calculado es el modelo de tejido ideal (dado que todas las células son iguales, cuando se expanden, sus límites tienden a formar un diagrama de Voronoy).

A partir de aquí, los investigadores miden qué tan similares son los tejidos a una muestra real. Si son iguales, los verdaderos tejidos están sanos.. De lo contrario, algunas células no tienen las mismas características físicas que sus vecinas, lo que puede indicar el inicio de un proceso tumoral.

Dudar siempre dudar

Los biólogos no están convencidos de esta hipótesis generalmente aceptada. Construyeron un modelo matemático para una tubería nuevamente basado en diagramas de Voronoy Donde las células cambian de vecino de una superficie a otra. Los especialistas dicen: “Lo más importante es que el modelo fue capaz de predecir lo que sucedía en la naturaleza”. Después de examinar las muestras de células epiteliales de las glándulas salivales de la mosca de la fruta, comprobaron que las células reales tenían la misma forma que en el modelo.

Se necesitaba una forma geométrica para modelar bien las células del tejido epitelial. Se puede plegar y adoptar diferentes curvas. Su forma corresponde al modelo de balance de potencia. Fue desde la superficie basal hasta la apical, pero sin tener los mismos contactos en ambas superficies.

La solución final sugerida fue Ascotoide. Estas formas recordaban la disposición de dos regiones del pecho de algunos insectos: el escudo y el tallo. “La similitud es muy grande para los escarabajos Protaetia speciosa, Indica en el documento.

Para dar equilibrio La vista tridimensional requería la interacción entre biólogos (Que son capaces de describir con precisión cómo se colocan los tejidos), matemáticos (que encuentran la formulación matemática adecuada adaptada a las descripciones proporcionadas por la anterior) y físicos (que verifican que la estructura descrita es posible en el sentido de un equilibrio de fuerzas). Para llegar al modelo final, fue necesario verificar que las predicciones hechas por el modelo fueron modificadas para coincidir con la realidad.

El ascotoide se obtiene a partir de secciones verticales en todas las superficies entre las superficies apical y basal. Por ejemplo, se selecciona un conjunto de puntos (semillas) en la superficie apical. En cada una de estas semillas se dibujan porciones perpendiculares a la superficie apical. En cada capa entre mis ápices y la base, cada fracción producirá un cruce (nueva semilla). Estas nuevas semillas se calculan utilizando el diagrama de Voronoy en esa capa. Finalmente, se fijan las regiones de Voronoi (que serán polígonos) correspondientes a todos los puntos del mismo segmento.

Su forma

El escutoide es un sólido geométrico entre dos superficies paralelas (basal y apical), por lo que la intersección del ascotoide en ambas superficies (y también en el resto de las capas intermedias) son polígonos (que serán las “cimas” del escutoide). Los vértices de estos dos polígonos están conectados por una curva o conexión en forma de Y.

Las caras no tienen por qué ser convexas. Puede tener huecos internos o externos, por lo que se pueden llenar muchos cilindros para llenar el espacio completo entre las dos superficies paralelas. ¿Por qué la naturaleza es tan complicada? La respuesta viene del físico del equipo, Javier Busita, de los Departamentos de Bioingeniería, Ingeniería Química y Biomolecular de la Universidad de Lehigh en Pensilvania (EE. UU.). “Cambiar la forma no es gratis para las células: cuesta energía. También hay que empaquetarlos juntos, ya que hay que invertir, por ejemplo, en producir partículas que actúen como pegamento. Sin embargo, las células siempre buscan ahorrar energía. Si se cuenta el costo de la pasta. Con las celdas juntas planas a niveladas, se verificará que la tapa es la mejor opción de empaque para guardar cuando hay algo de flexión en los tejidos.

El concepto se relaciona con la búsqueda del equilibrio de fuerzas al que están sujetas las células desde el punto de vista de la tensión. De esta manera elegante, matemáticas, biología y física van de la mano en este descubrimiento. Los resultados experimentales se confirmaron en otros tejidos epiteliales curvos, como la superficie de la mosca y un embrión de pez cebra. Esto fue necesario para generalizar las conclusiones.

El conocimiento en este detalle de la estructura de las células epiteliales puede ser necesario para el establecimiento de órganos in vitro. Aún nos queda un largo camino por recorrer, pero se está avanzando mucho gracias a los cultivos orgánicos y las versiones simplificadas de órganos cada vez más relacionados.

Con organelos Las enfermedades se pueden estudiar en platos de cultivo. “A través de nuestro trabajo hemos sentado las bases para estudiar si los orgánulos están empaquetados correctamente y, en consecuencia, reproducir fielmente las características del órgano que utilizas como modelo ”, dicen los especialistas.

Sigue leyendo:

Aire limpio, el mejor aliado para reducir la propagación del COVID-19

Claves de la nueva mutación del SARS-CoV-2, según un experto de Malbrán